6.5 – Heat of Reaction and Formation Methods

6.5.0 – Learning Objectives

By the end of this section you should be able to:

  1. Understand when you should use heat of reaction method.
  2. Understand when you should use heat of formation method.
  3. Solve a problem using heat of reaction method.
  4. Solve a problem using heat of formation method.

6.5.1 – Introduction

There are two common methods to solving energy balances. The first is heat of reaction method. This method is generally preferred for a single reaction sys where \(\Delta H_r\) is known. The second method is heat of formation method. This method is generally preferred for multiple reactions and systems where \(\Delta H_r\) is not readily available.

6.5.2 – Heat of Reaction Method

There are seven steps to solving an energy balance using the heat of reaction method:

  1. Solve the material balances as much as possible.
  2. Choose reference states for energy calculations.
  3. Calculate the extent of reaction for all reactions.
  4. Prepare the inlet/outlet enthalpy table.
  5. Calculate Enthalpies.
  6. Calculate \(\Delta \dot{H}\) for the reactor.
  7. Solve the energy balance.

Let’s try using this method to solve an energy balance. Suppose you are trying to solve how much heat is given off by the furnace shown below?

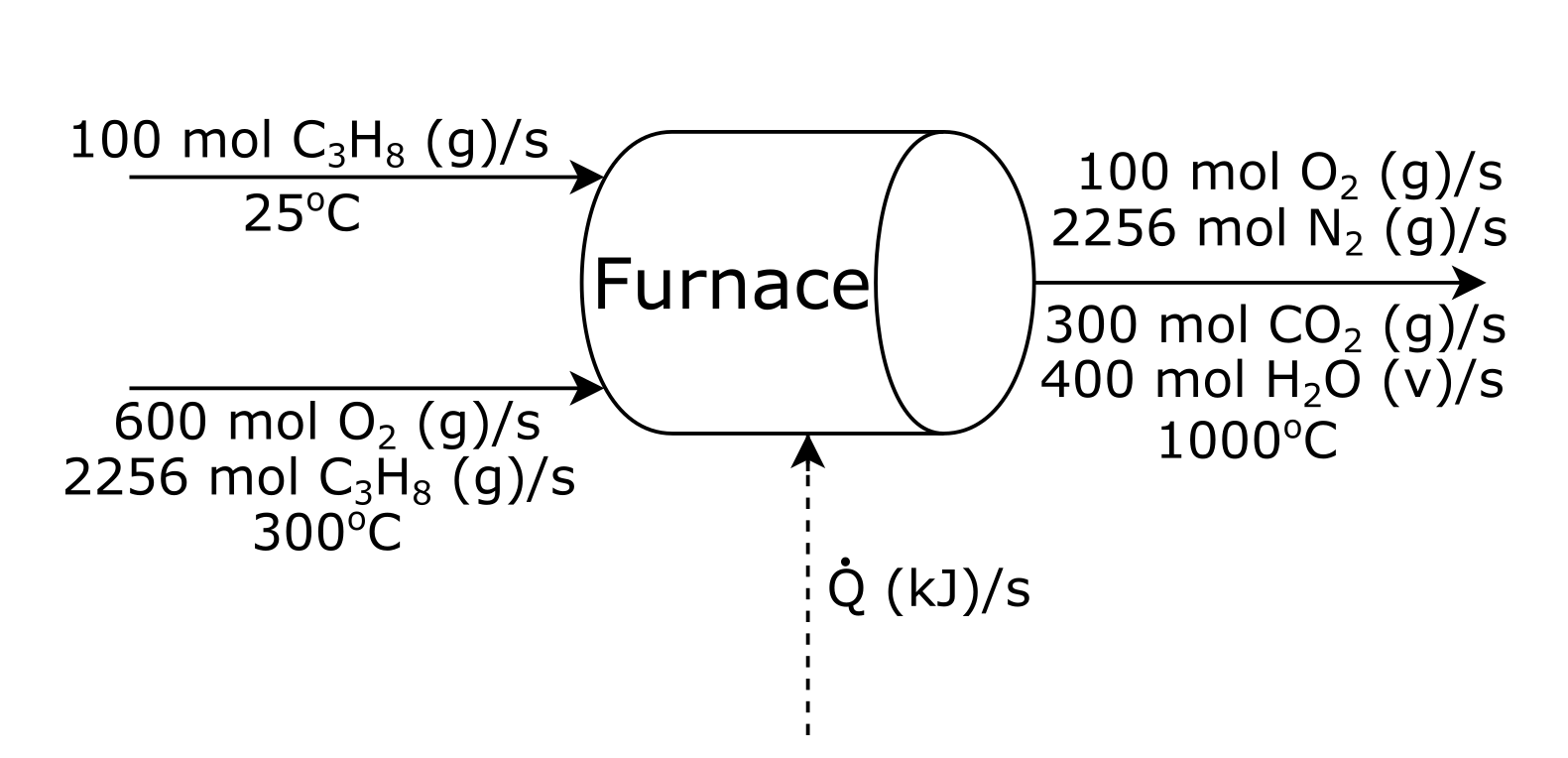
Attribution: Said Zaid-Alkailani & UBC [CC BY 4.0 de (https://creativecommons.org/licenses/by/4.0/)]

\[C_3 H_8 \small{\text{(g)}} + 5 \space O_2 \small{\text{(g)}} \longrightarrow 3 \space C O_2 \small{\text{(g)}} + 4 \space H_2 O \small{\text{(l)}} \quad \Delta H_r^o = -2220 kJ\]

1. Solve the material balances as much as possible:

In this problem, the material balance has already been solved

2. Choose reference states for energy calculations:

For the reacting species, \(C_3 H_8 \small{\text{(g)}}\), \(O_2 \small{\text{(g)}}\), \(C O_2 \small{\text{(g)}}\), \(H_2 O \small{\text{(l)}}\), we will choose \(25 ^{\circ} C\) and \(1\) atm as our reference state so that we have the same reference as the heat of reaction.

For the non-reacting species, \(N_2 \small{\text{(g)}}\), we will choose \(25 ^{\circ} C\) and \(1\) atm as our reference state because we have an enthalpy table.

3. Calculate the extent of reaction for all reactions:

In this case we have 1 reaction and can use the formula (for any compound involved in the reaction):

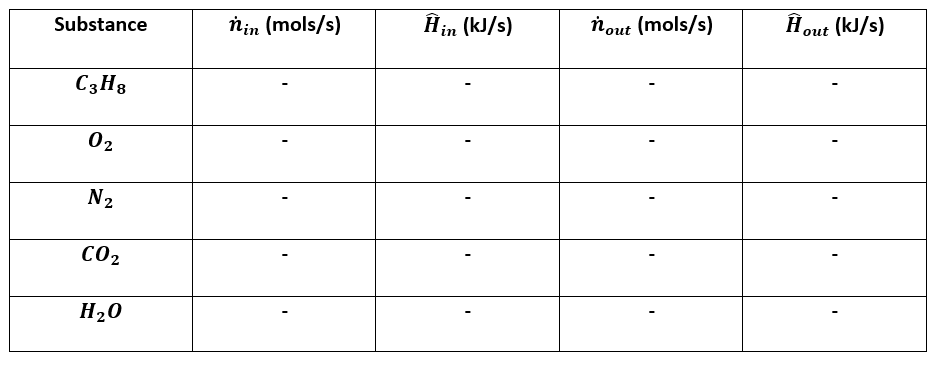
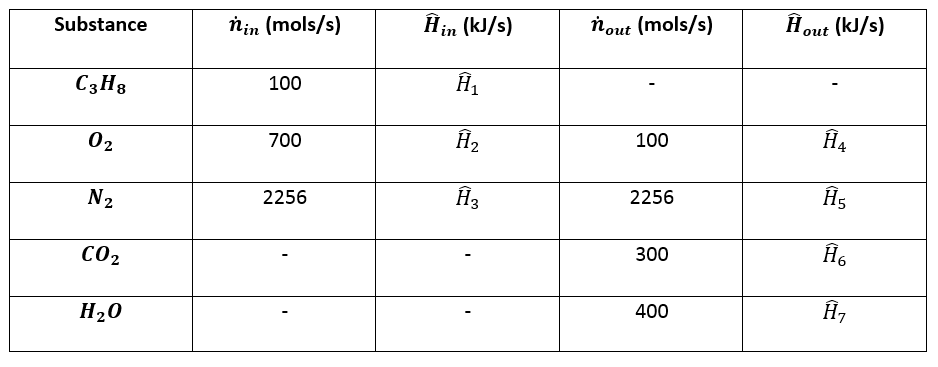
\[\xi = \frac{\mid (\dot{n}_i)_{out} - (\dot{n}_i)_{in} \mid}{\mid \dot{\nu}_i \mid}\]
\[\xi = \frac{\mid (\dot{n}_{C O_2})_{out} - (\dot{n}_{C O_2})_{in} \mid}{\mid \dot{\nu}_{C O_2} \mid} = \frac{\mid 300 - 0 \mid}{\mid 3 \mid} = 100\]

4. Prepare the inlet/outlet enthalpy table:

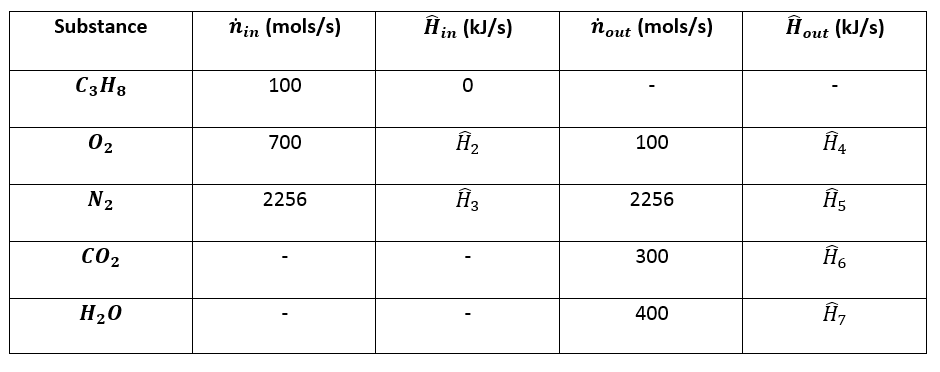
5. Calculate Enthalpies:

\[\]

\(\hat{H}_2 = \Delta \hat{H} \text{ for } O_2 \text{ from } 25 ^{\circ} C \text{ to } 300 ^{\circ} C = (8.47 - 0) \space kJ/mol = 8.47 \space kJ/mol\)

\(\hat{H}_3 = \Delta \hat{H} \text{ for } N_2 \text{ from } 25 ^{\circ} C \text{ to } 300 ^{\circ} C = (8.12 - 0) \space kJ/mol = 8.12 \space kJ/mol\)

\(\hat{H}_4 = \Delta \hat{H} \text{ for } O_2 \text{ from } 25 ^{\circ} C \text{ to } 1000 ^{\circ} C = (32.47 - 0) \space kJ/mol = 32.47 \space kJ/mol\)

\(\hat{H}_5 = \Delta \hat{H} \text{ for } N_2 \text{ from } 25 ^{\circ} C \text{ to } 1000 ^{\circ} C = (30.56 - 0) \space kJ/mol = 30.56 \space kJ/mol\)

\(\hat{H}_6 = \Delta \hat{H} \text{ for } C O_2 \text{ from } 25 ^{\circ} C \text{ to } 1000 ^{\circ} C = (48.60 - 0) \space kJ/mol = 48.60 \space kJ/mol\)

\(\hat{H}_7 = \Delta \hat{H} \text{ for } H_2 O \space (l, \space 25 ^{\circ} C) \rightarrow H_2 O \space (v, \space 1000 ^{\circ} C)\)

\(\hat{H}_7 = \int_{25 ^{\circ} C}^{100 ^{\circ} C} C_{pl} dT + \Delta \hat{H}_v (100 ^{\circ} C) + \int_{100 ^{\circ} C}^{1000 ^{\circ} C} C_{pv} dT = 81.46 kJ/mol\)

\[\]

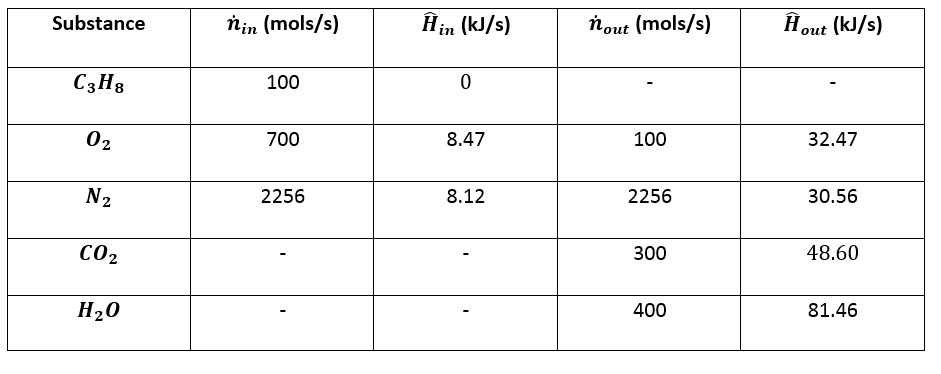
6. Calculate \(\Delta \dot{H}\) for the reactor:

\[\Delta \dot{H} = \xi \Delta \dot{H}_r ^{\circ} + \sum \dot{n}_{out} \cdot \hat{H}_{out} - \sum \dot{n}_{in} \cdot \hat{H}_{in}\]
\[\Delta \dot{H} = 100 \space mol/s \cdot 2220 \space kJ/mol + \sum \dot{n}_{out} \cdot \hat{H}_{out} - \sum \dot{n}_{in} \cdot \hat{H}_{in} = -1.26 \times 10^5 \space kJ/s\]

7. Solve the energy balance:

\[\Delta \dot{H} = -1.26 \times 10^5 \space kJ/s\]
\[\Delta \dot{H} + \Delta \dot{E}_k + \Delta \dot{E}_p = \dot{Q} + \dot{W}_s\]

where \(\Delta \dot{E}_k\), \(\Delta \dot{E}_p\), and \(\dot{W}_s\) are assumed to be negligible.

\[\therefore \space \dot{Q} = \Delta \dot{H} = -1.26 \times 10^5 \space kW\]

6.5.3 – Heat of Formation Method

There are six steps to solving an energy balance using the heat of formation method:

  1. Solve the material balances as much as possible.
  2. Choose reference states for energy calculations.
  3. Prepare the inlet/outlet enthalpy table.
  4. Calculate Enthalpies.
  5. Calculate \(\Delta \dot{H}\) for the reactor.
  6. Solve the energy balance.

Let’s try using this method to solve an energy balance. Suppose you are trying to solve how much heat is given off by the furnace shown below.

Attribution: Said Zaid-Alkailani & UBC [CC BY 4.0 de (https://creativecommons.org/licenses/by/4.0/)]

\[C_3 H_8 \small{\text{(g)}} + 5 \space O_2 \small{\text{(g)}} \longrightarrow 3 \space C O_2 \small{\text{(g)}} + 4 \space H_2 O \small{\text{(l)}} \quad \Delta H_r^o = ?\]

1. Solve the material balances as much as possible:

In this problem, the material balance has already been solved

2. Choose reference states for energy calculations:

For the reacting species, we must find their elemental species at standard condition. The elemental species for \(C_3 H_8 \small{\text{(g)}}\), \(O_2 \small{\text{(g)}}\), \(C O_2 \small{\text{(g)}}\), and \(H_2 O \small{\text{(l)}}\) are \(C \small{\text{(s)}}\), \(H_2 \small{\text{(g)}}\) and \(O_2 \small{\text{(g)}}\). We will choose \(25 ^{\circ} C\) and \(1\) atm as our reference state for these elemental species.

For the non-reacting species, \(N_2 \small{\text{(g)}}\), we will choose \(25 ^{\circ} C\) and \(1\) atm as our reference state because we have an enthalpy table.

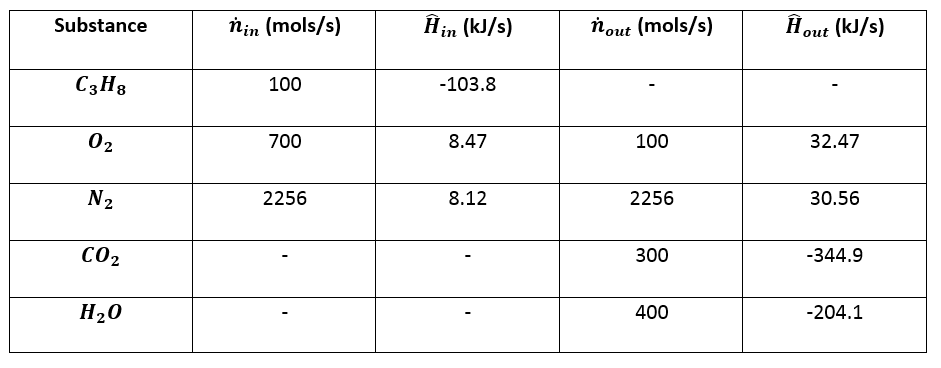
3. Prepare the inlet/outlet enthalpy table:

4. Calculate Enthalpies:

\[\]

\(\hat{H}_1 = \Delta \hat{H}_{f, \space C_3 H_8 \small{\text{(g)}}} ^{\circ} = -103.8 \space kJ/mol\)

\(\hat{H}_2 = \Delta \hat{H} \text{ for } O_2 \text{ from } 25 ^{\circ} C \text{ to } 300 ^{\circ} C = (8.47 - 0) \space kJ/mol = 8.47 \space kJ/mol\)

\(\hat{H}_3 = \Delta \hat{H} \text{ for } N_2 \text{ from } 25 ^{\circ} C \text{ to } 300 ^{\circ} C = (8.12 - 0) \space kJ/mol = 8.12 \space kJ/mol\)

\(\hat{H}_4 = \Delta \hat{H} \text{ for } O_2 \text{ from } 25 ^{\circ} C \text{ to } 1000 ^{\circ} C = (32.47 - 0) \space kJ/mol = 32.47 \space kJ/mol\)

\(\hat{H}_5 = \Delta \hat{H} \text{ for } N_2 \text{ from } 25 ^{\circ} C \text{ to } 1000 ^{\circ} C = (30.56 - 0) \space kJ/mol = 30.56 \space kJ/mol\)

\(\hat{H}_6 = \Delta \hat{H}_{f, \space C O_2 \small{\text{(g)}}} ^{\circ} + \int_{25 ^{\circ} C}^{1000 ^{\circ} C} C_{p, \space C O_2 \small{\text{(g)}}} dT = -344.9 \space kJ/mol\)

\(\hat{H}_7 = \Delta \hat{H}_{f, \space H_2 O \small{\text{(v)}}} ^{\circ} + \int_{25 ^{\circ} C}^{1000 ^{\circ} C} C_{p, \space H_2 O \small{\text{(v)}}} dT = -204.1 \space kJ/mol\)

\[\]

5. Calculate \(\Delta \dot{H}\) for the reactor:

\[\Delta \dot{H} = \sum \dot{n}_{out} \cdot \hat{H}_{out} - \sum \dot{n}_{in} \cdot \hat{H}_{in} = -1.26 \times 10^5 \space kJ/s\]

6. Solve the energy balance:

\[\Delta \dot{H} = -1.26 \times 10^5 \space kJ/s\]
\[\Delta \dot{H} + \Delta \dot{E}_k + \Delta \dot{E}_p = \dot{Q} + \dot{W}_s\]

where \(\Delta \dot{E}_k\), \(\Delta \dot{E}_p\), and \(\dot{W}_s\) are assumed to be negligible.

\[\therefore \space \dot{Q} = \Delta \dot{H} = -1.26 \times 10^5 \space kW\]
In [ ]: